L01 Worksheet
1. 信息和熵
-
A. 给你一个未知的 3 位二进制数。然后你会被告知二进制表示恰好包含两个 1。您获得了多少信息?
\[ p = 3/8 \\ I = log_2(8/3) = log_2(8) - log_2(3) \approx 1.415 \] -
B. 额外信息,数字是奇数,获得了多少额外信息?
\[ I = log_2(3/2) = log_2(3) - log_2(2) \approx 0.585 \] -
C. X 代表一个不公平的硬币,其中 p(head) = 0.6。请计算 H(X)
\[ p(HEADS) = 0.6 \\ p(TAILS) = 1 - p(HEADS) \\ \]\[ H(X) = p(HEADS)*I(HEADS) + p(TAILS)*I(TAILS) \] -
D. 随机选择一个十进制数字,并告诉您其值 mod 3 为 0。您了解了多少关于该数字的信息?
\[ I = \log_2(10) - \log_2(4) \] -
E. X 是一个未知的 8 位二进制数。现在告诉你 X 和
10101100的汉明距离为 1。你获取了多少 bit 位的信息。\[ I = log_2(2^7/8) = 7 - 3 = 4 \] -
F. 对于 4 个概率不均匀的字母及编码,如果告诉你 “不是d” 这个消息值多少 bit?
符号 概率 编码 a 0.5 000000 b 0.125 11100 c 0.25 11011 d 0.125 10111 \[ p(!d) = 1 - 0.125 = 0.875 \\ I = log_2(\frac{1}{p}) = log_2(\frac{1}{0.875}) \\ = log_2(\frac{1}{\frac{7}{8}})= log_2(\frac{8}{7}) \\ = 3 - log_2(7) \approx 0.193 bits \] -
G. 如果你长期观察这个信号源,平均每一个符号能带给你多少比特的“惊喜”?
- a: $ p = 0.5, I = log_2(1/0.5) = 1 $
- b: $ p = 0.125, I = log_2(1/0.125) = 3 $
- c: $ p = 0.25, I = log_2(1/0.25) = 2 $
- d: $ p = 0.125, I = log_2(1/0.125) = 3 $
所以 $ H = \sum p \cdot I = 1.75 $
-
H. 给你一个 5 位二进制数,告诉你第一个和最后一个位数相等,你得到了多少信息?
\[ I = log_2(1/0.5) = 1 \] -
I. 我随机从字母表中选择一个字母并且告诉你我的选择不是"X", "Y" 也不是 “Z”。你获得了多少信息
\[ p = 23/26 \\ I = log_2(1/p) \approx 0.178 \] -
J. 对于一个随机 4 位补码数字,告诉你是正数,信息量多少。
\[ p = 7/16 \\ I = log_2(16/7) \]
补码
-
A. 6 位十进制 -21 的补码表示?
$$ 21 = 16 + 4 + 1 = 2^4 + 2^2 + 1 $$ 二进止表示为
010101取反加1为101011 -
B. 8 位补码 -51 的十六进制表示
8 位补码的表示范围是
-2^7 ~ 2^7-1即-128 ~ 127,没有溢出 $$ 51 = 32 + 16 + 2 + 1 = 2^5 + 2^4 + 2^1 + 2^0 $$ 补码表示为00110011取反加 1 为11001101十六进制为CD -
C. 8 位补码的十六进制是
0xD6,十进制是多少0xD6的二进制表示为11010110,说明是一个负数,采用负权重法 $$ -128+64+16+4+2 = -42 $$ -
D. 自1988年开始进行官方投球统计以来,单场比赛的最高投球数为172个。假设这 仍然是投球数的上限,那么我们需要多少位来将每场比赛的投球数记录为补码二进制数
$$ 2^7 < 172 < 2^8 $$ 所以至少需要 9 位,表示范围为 \(-2^8 ... 2^8-1\)
-
E. 两个补码数
0xB3 + 0x47的和的值可以用 8 位补码表示法来表示吗? 如果是这 样,其十六进制的总和是多少? 如果没有,请写“NO”按照十六进制加法
0xB3 + 0x47 = 0xFA,没有溢出,-6 -
F.两个2的补码0xB3 + 0xB1的和的值可以用8位补码表示法来表示吗? 如果是这 样,十六进制的总和是多少?如果没有,请写“NO”。
0xB3 + 0xB1 = 0x164溢出,NO -
G. 请使用 8 位二进制补码算术计算表达式 0xBB - 8 的值,并以十进制形式给出结果(基数为 10)
0xBB - 8 = 0xB3 = 11+3 = 14 -
H. 可以表示为 8 位二进制补码整数的最小(最大负数)整数是多少? 以十进制整数形式给出你的答案。
\[ -2^8 = -256 \] -
I. 以下运算在 8 位加法器上执行。 给出每个生成的 8 位总和(以十六进制表示)
0xF0 + 0x34 = 0x34 0xF0 + 0x80 = 0x80 -
J. 用 5 位二进制补码表示,单个 5 位数量可以表示的整数范围是多少?
\[ -2^4 ... 2^4-1 \] -
K. 考虑以下减法问题,其中操作数是 5 位二进制补码数。 计算结果并以十进制(以 10 为基数)形式给出答案。10101 − 00011
减一个数可以看作加上一个数的负数,取负数表示为 10101 - 00011 = 10101 + 11101 = 110010, 结果为 -2^4 + 2 = -14
什么情况下会溢出? 只有两个数同号,且结果为不同号时才发生溢出
在电路里 \(V = C_{in} C_{out}\)
\(C_{in}\) 表示最高位的进位
\(C_{out}\) 表示最高位向外产生的进位
如果发生溢出,两者必然一个是 1,另一个是 0
3. 可变长编码
-
A. 变量 X 可以表示为 A,B,C或D,以下是他们的概率,如果使用霍夫曼编码对该变量进行编码,则每个符号的编码中有多少位?
A 0.5 B 0.3 C 0.1 D 0.1 使用 huffman 编码 ||| |--|--| |A| 0| |B |11| |C| 100| |D |101|
\(H = 1*0.5 + 2*.03 + 3*0.2 = 0.5+0.6+0.6 = 1.7\)
\[ 0.5*log_2(1/0.5) + 0.3*log_2(1/0.3) + 0.1*log_2(1/0.1) + 0.1*log_2(1/0.1) \\ \approx 1.685 \]根据概率,判断以下属于概率可能对应哪个树,选择霍夫曼编码树或通过对这些概率分布运行霍夫曼算法而产生的树
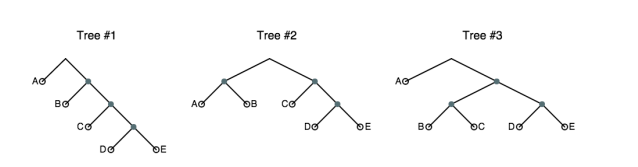
-
B. p(A) = 0.3, p(B) = 0.3, p(C) = 0.2, p(D) = 0.1, p(E) = 0.1
Tree(s): 2
-
C.